Chapter 5 and tidymodels

Tyler George

Cornell College
STA 362 Spring 2024 Block 8

Setup

library(tidyverse)
library(ISLR)
library(tidymodels)
library(gridExtra)

Cross validation

💡 Big idea

• We have determined that it is sensible to use a test set to calculate metrics like prediction error

Cross validation

💡 Big idea

• We have determined that it is sensible to use a test set to calculate metrics like prediction error

Why?

Cross validation

💡 Big idea

• We have determined that it is sensible to use a test set to calculate metrics like prediction error

How could we do this?

Cross validation

💡 Big idea

• We have determined that it is sensible to use a test set to calculate metrics like prediction error
• What if we don’t have a separate data set to test our model on?
• 🎉 We can use resampling methods to estimate the test-set prediction error

Training error versus test error

What is the difference? Which is typically larger?

• The training error is calculated by using the same observations used to fit the statistical learning model
• The test error is calculated by using a statistical learning method to predict the response of new observations
• The training error rate typically underestimates the true prediction error rate

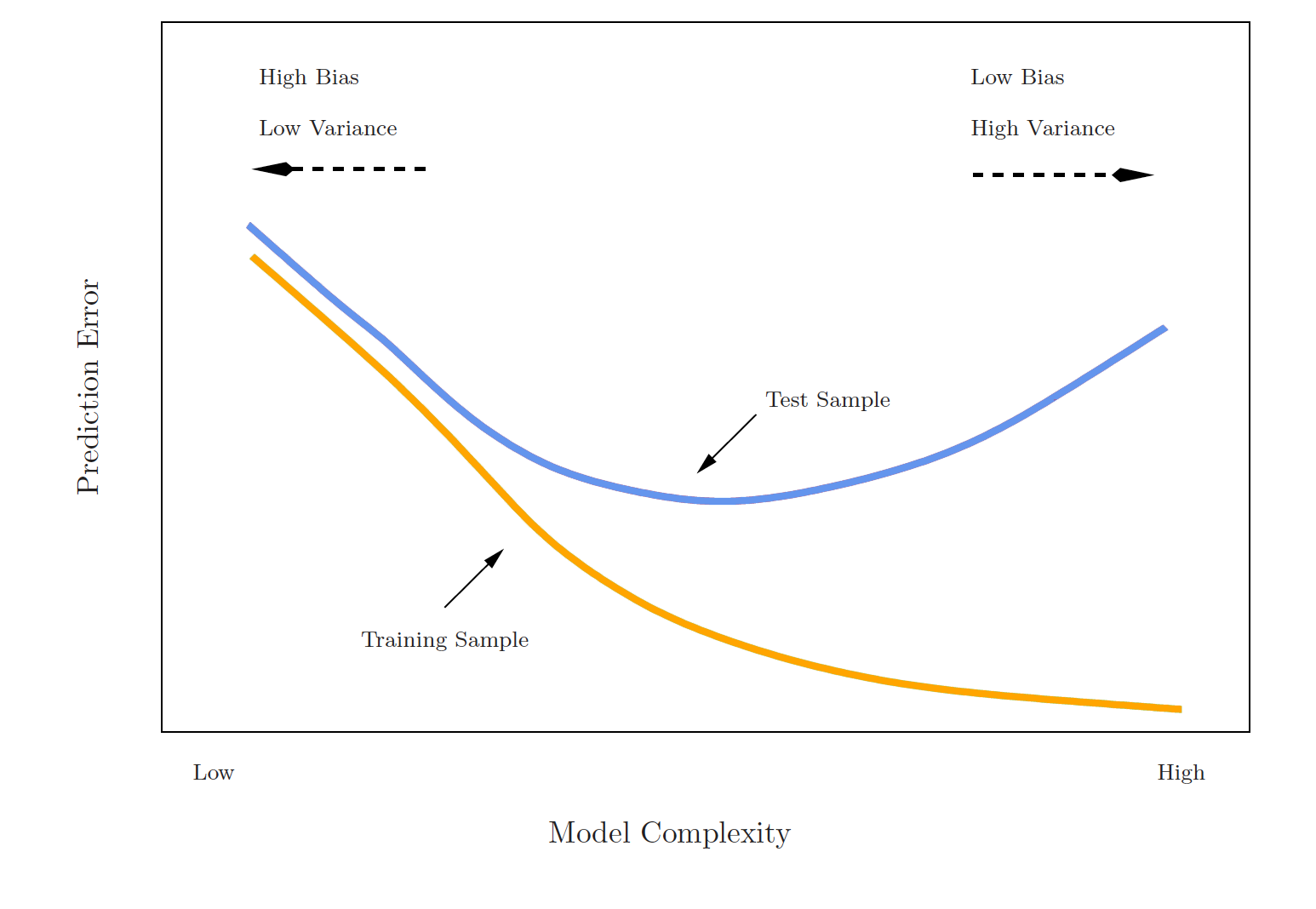
Estimating prediction error

• Best case scenario: We have a large data set to test our model on
• This is not always the case!

💡 Let’s instead find a way to estimate the test error by holding out a subset of the training observations from the model fitting process, and then applying the statistical learning method to those held out observations

Approach #1: Validation set

• Randomly divide the available set up samples into two parts: a training set and a validation set
• Fit the model on the training set, calculate the prediction error on the validation set

If we have a quantitative predictor what metric would we use to calculate this test error?

• Often we use Mean Squared Error (MSE)

Approach #1: Validation set

• Randomly divide the available set up samples into two parts: a training set and a validation set
• Fit the model on the training set, calculate the prediction error on the validation set

If we have a qualitative predictor what metric would we use to calculate this test error?

• Often we use misclassification rate

Approach #1: Validation set

\[\Large\color{orange}{MSE_{\texttt{test-split}} = \textrm{Ave}_{i\in\texttt{test-split}}[y_i-\hat{f}(x_i)]^2}\]

\[\Large\color{orange}{Err_{\texttt{test-split}} = \textrm{Ave}_{i\in\texttt{test-split}}I[y_i\neq \mathcal{\hat{C}}(x_i)]}\]

Approach #1: Validation set

Auto example:

• We have 392 observations.
• Trying to predict mpg from horsepower.
• We can split the data in half and use 196 to fit the model and 196 to test

Approach #1: Validation set

\(\color{orange}{MSE_{\texttt{test-split}}}\)

\(\color{orange}{MSE_{\texttt{test-split}}}\)

\(\color{orange}{MSE_{\texttt{test-split}}}\)

\(\color{orange}{MSE_{\texttt{test-split}}}\)

Approach #1: Validation set

Auto example:

• We have 392 observations.
• Trying to predict mpg from horsepower.
• We can split the data in half and use 196 to fit the model and 196 to test - what if we did this many times?

Approach #1: Validation set (Drawbacks)

• the validation estimate of the test error can be highly variable, depending on which observations are included in the training set and which observations are included in the validation set
• In the validation approach, only a subset of the observations (those that are included in the training set rather than in the validation set) are used to fit the model
• Therefore, the validation set error may tend to overestimate the test error for the model fit on the entire data set

Approach #2: K-fold cross validation

💡 The idea is to do the following:

• Randomly divide the data into \(K\) equal-sized parts
• Leave out part \(k\), fit the model to the other \(K - 1\) parts (combined)
• Obtain predictions for the left-out \(k\)th part
• Do this for each part \(k = 1, 2,\dots K\), and then combine the result

K-fold cross validation

\(\color{orange}{MSE_{\texttt{test-split-1}}}\)

\(\color{orange}{MSE_{\texttt{test-split-2}}}\)

\(\color{orange}{MSE_{\texttt{test-split-3}}}\)

\(\color{orange}{MSE_{\texttt{test-split-4}}}\)

Take the mean of the \(k\) MSE values

Application Exercise

Create a new R project, then a new quarto file with cv in its name in that project. Answer the questions in that file.

If we use 10 folds:

1. What percentage of the training data is used in each analysis for each fold?
2. What percentage of the training data is used in the assessment for each fold?

countdown::countdown(2)

02:00

Estimating prediction error (quantitative outcome)

• Split the data into K parts, where \(C_1, C_2, \dots, C_k\) indicate the indices of observations in part \(k\)
• \(CV_{(K)} = \sum_{k=1}^K\frac{n_k}{n}MSE_k\)
• \(MSE_k = \sum_{i \in C_k} (y_i - \hat{y}_i)^2/n_k\)
• \(n_k\) is the number of observations in group \(k\)
• \(\hat{y}_i\) is the fit for observation \(i\) obtained from the data with the part \(k\) removed
• If we set \(K = n\), we’d have \(n-fold\) cross validation which is the same as leave-one-out cross validation (LOOCV)

Estimating prediction error (quantitative outcome)

• Split the data into K parts, where \(C_1, C_2, \dots, C_k\) indicate the indices of observations in part \(k\)
• \(CV_{(K)} = \sum_{k=1}^K\frac{n_k}{n}MSE_k\)
• \(MSE_k = \sum_{i \in C_k} (y_i - \hat{y}_i)^2/n_k\)
• \(n_k\) is the number of observations in group \(k\)
• \(\hat{y}_i\) is the fit for observation \(i\) obtained from the data with the part \(k\) removed
• If we set \(K = n\), we’d have \(n-fold\) cross validation which is the same as leave-one-out cross validation (LOOCV)

Leave-one-out cross validation

\(\dots\)

Special Case!

• With linear regression, you can actually calculate the LOOCV error without having to iterate!
• \(CV_{(n)} = \frac{1}{n}\sum_{i=1}^n\left(\frac{y_i-\hat{y}_i}{1-h_i}\right)^2\)
• \(\hat{y}_i\) is the \(i\)th fitted value from the linear model
• \(h_i\) is the diagonal of the “hat” matrix (remember that! 🎓)

Picking \(K\)

• \(K\) can vary from 2 (splitting the data in half each time) to \(n\) (LOOCV)
• LOOCV is sometimes useful but usually the estimates from each fold are very correlated, so their average can have a high variance
• A better choice tends to be \(K=5\) or \(K=10\)

Bias variance trade-off

• Since each training set is only \((K - 1)/K\) as big as the original training set, the estimates of prediction error will typically be biased upward
• This bias is minimized when \(K = n\) (LOOCV), but this estimate has a high variance
• \(K =5\) or \(K=10\) provides a nice compromise for the bias-variance trade-off

Approach #2: K-fold Cross Validation

Auto example:

• We have 392 observations.
• Trying to predict mpg from horsepower

Estimating prediction error (qualitative outcome)

• The premise is the same as cross valiation for quantitative outcomes
• Split the data into K parts, where \(C_1, C_2, \dots, C_k\) indicate the indices of observations in part \(k\)
• \(CV_K = \sum_{k=1}^K\frac{n_k}{n}Err_k\)
• \(Err_k = \sum_{i\in C_k}I(y_i\neq\hat{y}_i)/n_k\) (misclassification rate)
• \(n_k\) is the number of observations in group \(k\)
• \(\hat{y}_i\) is the fit for observation \(i\) obtained from the data with the part \(k\) removed

Estimating prediction error (qualitative outcome)

• The premise is the same as cross valiation for quantitative outcomes
• Split the data into K parts, where \(C_1, C_2, \dots, C_k\) indicate the indices of observations in part \(k\)
• \(CV_K = \sum_{k=1}^K\frac{n_k}{n}Err_k\)
• \(Err_k = \sum_{i\in C_k}I(y_i\neq\hat{y}_i)/n_k\) (misclassification rate)
• \(n_k\) is the number of observations in group \(k\)
• \(\hat{y}_i\) is the fit for observation \(i\) obtained from the data with the part \(k\) removed

tidymodels

Application Exercise

1. Create a new quarto file in your project and add tidymodels in the name.

2. Load the packages by running the top chunk of R code

library(tidymodels)
library(broom)
library(ISLR)
library(countdown)

tidymodels

tidymodels.org

• tidymodels is an opinionated collection of R packages designed for modeling and statistical analysis.
• All packages share an underlying philosophy and a common grammar.

Step 1: Specify the model

• Pick the model
• Set the engine

Specify the model

linear_reg() |>
  set_engine("lm")

Specify the model

linear_reg() |>
  set_engine("glmnet")

Specify the model

linear_reg() |>
  set_engine("spark")

Specify the model

decision_tree() |>
  set_engine("rpart")

Specify the model

• All available models:

tidymodels.org

Application Exercise

1. Write a pipe that creates a model that uses lm() to fit a linear regression using tidymodels. Save it as lm_spec and look at the object. What does it return?

Hint: you’ll need https://www.tidymodels.org

05:00

Answer

lm_spec <- 
  linear_reg() |> # Pick linear regression
  set_engine(engine = "lm") # set engine
lm_spec

Linear Regression Model Specification (regression)

Computational engine: lm 

Fit the data

• You can train your model using the fit() function

fit(lm_spec,
    mpg ~ horsepower,
    data = Auto)

parsnip model object


Call:
stats::lm(formula = mpg ~ horsepower, data = data)

Coefficients:
(Intercept)   horsepower  
    39.9359      -0.1578  

Application Exercise

1. Fit the model:

library(ISLR)
lm_fit <- fit(lm_spec,
              mpg ~ horsepower,
              data = Auto)
lm_fit

Does this give the same results as

lm(mpg ~ horsepower, data = Auto)

03:00

Answer

lm_fit <- fit(lm_spec,
              mpg ~ horsepower,
              data = Auto)
lm_fit

parsnip model object


Call:
stats::lm(formula = mpg ~ horsepower, data = data)

Coefficients:
(Intercept)   horsepower  
    39.9359      -0.1578  

lm(mpg ~ horsepower, data = Auto)

Call:
lm(formula = mpg ~ horsepower, data = Auto)

Coefficients:
(Intercept)   horsepower  
    39.9359      -0.1578  

Get predictions

lm_fit |>
  predict(new_data = Auto)

• Uses the predict() function
• ‼️ new_data has an underscore
• 😄 This automagically creates a data frame

Get predictions

lm_fit |>
  predict(new_data = Auto) |>
  bind_cols(Auto)

# A tibble: 392 × 10
   .pred   mpg cylinders displacement horsepower weight acceleration  year origin name    
 * <dbl> <dbl>     <dbl>        <dbl>      <dbl>  <dbl>        <dbl> <dbl>  <dbl> <fct>   
 1 19.4     18         8          307        130   3504         12      70      1 chevrol…
 2 13.9     15         8          350        165   3693         11.5    70      1 buick s…
 3 16.3     18         8          318        150   3436         11      70      1 plymout…
 4 16.3     16         8          304        150   3433         12      70      1 amc reb…
 5 17.8     17         8          302        140   3449         10.5    70      1 ford to…
 6  8.68    15         8          429        198   4341         10      70      1 ford ga…
 7  5.21    14         8          454        220   4354          9      70      1 chevrol…
 8  6.00    14         8          440        215   4312          8.5    70      1 plymout…
 9  4.42    14         8          455        225   4425         10      70      1 pontiac…
10  9.95    15         8          390        190   3850          8.5    70      1 amc amb…
# ℹ 382 more rows

What does bind_cols do?

Get predictions

lm_fit |>
  predict(new_data = Auto) |>
  bind_cols(Auto)

# A tibble: 392 × 10
   .pred   mpg cylinders displacement horsepower weight acceleration  year origin name    
 * <dbl> <dbl>     <dbl>        <dbl>      <dbl>  <dbl>        <dbl> <dbl>  <dbl> <fct>   
 1 19.4     18         8          307        130   3504         12      70      1 chevrol…
 2 13.9     15         8          350        165   3693         11.5    70      1 buick s…
 3 16.3     18         8          318        150   3436         11      70      1 plymout…
 4 16.3     16         8          304        150   3433         12      70      1 amc reb…
 5 17.8     17         8          302        140   3449         10.5    70      1 ford to…
 6  8.68    15         8          429        198   4341         10      70      1 ford ga…
 7  5.21    14         8          454        220   4354          9      70      1 chevrol…
 8  6.00    14         8          440        215   4312          8.5    70      1 plymout…
 9  4.42    14         8          455        225   4425         10      70      1 pontiac…
10  9.95    15         8          390        190   3850          8.5    70      1 amc amb…
# ℹ 382 more rows

Which column has the predicted values?

Application Exercise

03:00

1. Edit the code below to add the original data to the predicted data.

mpg_pred <- lm_fit |> 
  predict(new_data = Auto) |> 
  ---

Get predictions

mpg_pred <- lm_fit |>
  predict(new_data = Auto) |>
  bind_cols(Auto)

mpg_pred

# A tibble: 392 × 10
   .pred   mpg cylinders displacement horsepower weight acceleration  year origin name    
 * <dbl> <dbl>     <dbl>        <dbl>      <dbl>  <dbl>        <dbl> <dbl>  <dbl> <fct>   
 1 19.4     18         8          307        130   3504         12      70      1 chevrol…
 2 13.9     15         8          350        165   3693         11.5    70      1 buick s…
 3 16.3     18         8          318        150   3436         11      70      1 plymout…
 4 16.3     16         8          304        150   3433         12      70      1 amc reb…
 5 17.8     17         8          302        140   3449         10.5    70      1 ford to…
 6  8.68    15         8          429        198   4341         10      70      1 ford ga…
 7  5.21    14         8          454        220   4354          9      70      1 chevrol…
 8  6.00    14         8          440        215   4312          8.5    70      1 plymout…
 9  4.42    14         8          455        225   4425         10      70      1 pontiac…
10  9.95    15         8          390        190   3850          8.5    70      1 amc amb…
# ℹ 382 more rows

Calculate the error

• Root mean square error

mpg_pred |>
  rmse(truth = mpg, estimate = .pred)

# A tibble: 1 × 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 rmse    standard        4.89

What is this estimate? (training error? testing error?)

Validation set approach

Auto_split <- initial_split(Auto, prop = 0.5)
Auto_split

<Training/Testing/Total>
<196/196/392>

How many observations are in the training set?

Validation set approach

Auto_split <- initial_split(Auto, prop = 0.5)
Auto_split

<Training/Testing/Total>
<196/196/392>

How many observations are in the test set?

Validation set approach

Auto_split <- initial_split(Auto, prop = 0.5)
Auto_split

<Training/Testing/Total>
<196/196/392>

How many observations are there in total?

Validation set approach

Auto_split <- initial_split(Auto, prop = 0.5)
Auto_split

<Training/Testing/Total>
<196/196/392>

• Extract the training and testing data

training(Auto_split)
testing(Auto_split)

Validation set approach

Auto_train <- training(Auto_split)

Auto_train

# A tibble: 196 × 9
     mpg cylinders displacement horsepower weight acceleration  year origin name          
   <dbl>     <dbl>        <dbl>      <dbl>  <dbl>        <dbl> <dbl>  <dbl> <fct>         
 1  37.7         4           89         62   2050         17.3    81      3 toyota tercel 
 2  27           4           97         60   1834         19      71      2 volkswagen mo…
 3  22           6          232        112   2835         14.7    82      1 ford granada l
 4  16           6          250        100   3781         17      74      1 chevrolet che…
 5  25           4           90         71   2223         16.5    75      2 volkswagen da…
 6  18           6          232        100   2945         16      73      1 amc hornet    
 7  38.1         4           89         60   1968         18.8    80      3 toyota coroll…
 8  23           4           97         54   2254         23.5    72      2 volkswagen ty…
 9  15           8          302        130   4295         14.9    77      1 mercury couga…
10  34           4          108         70   2245         16.9    82      3 toyota corolla
# ℹ 186 more rows

Application Exercise

1. Copy the code below, fill in the blanks to fit a model on the training data then calculate the test RMSE.

set.seed(100)
Auto_split  <- ________
Auto_train  <- ________
Auto_test   <- ________
lm_fit      <- fit(lm_spec, 
                   mpg ~ horsepower, 
                   data = ________)
mpg_pred  <- ________ |> 
  predict(new_data = ________) |> 
  bind_cols(________)
rmse(________, truth = ________, estimate = ________)

06:00

A faster way!

• You can use last_fit() and specify the split
• This will automatically train the data on the train data from the split
• Instead of specifying which metric to calculate (with rmse as before) you can just use collect_metrics() and it will automatically calculate the metrics on the test data from the split

A faster way!

set.seed(100)

Auto_split <- initial_split(Auto, prop = 0.5)
lm_fit <- last_fit(lm_spec,
                   mpg ~ horsepower,
                   split = Auto_split) 

lm_fit |>
  collect_metrics()

# A tibble: 2 × 4
  .metric .estimator .estimate .config             
  <chr>   <chr>          <dbl> <chr>               
1 rmse    standard       4.96  Preprocessor1_Model1
2 rsq     standard       0.613 Preprocessor1_Model1

A faster way!

set.seed(100)

Auto_split <- initial_split(Auto, prop = 0.5)
lm_fit <- last_fit(lm_spec,
                   mpg ~ horsepower,
                   split = Auto_split) 

lm_fit |>
  collect_metrics()

# A tibble: 2 × 4
  .metric .estimator .estimate .config             
  <chr>   <chr>          <dbl> <chr>               
1 rmse    standard       4.96  Preprocessor1_Model1
2 rsq     standard       0.613 Preprocessor1_Model1

What about cross validation?

Auto_cv <- vfold_cv(Auto, v = 5)
Auto_cv

#  5-fold cross-validation 
# A tibble: 5 × 2
  splits           id   
  <list>           <chr>
1 <split [313/79]> Fold1
2 <split [313/79]> Fold2
3 <split [314/78]> Fold3
4 <split [314/78]> Fold4
5 <split [314/78]> Fold5

What about cross validation?

• Instead of fit we will use fit_resamples

fit_resamples(lm_spec, 
              mpg ~ horsepower,
              resamples = Auto_cv) 

What about cross validation?

How do we get the metrics out? With collect_metrics() again!

results <- fit_resamples(lm_spec,
                         mpg ~ horsepower,
                         resamples = Auto_cv)

results |>
  collect_metrics()

# A tibble: 2 × 6
  .metric .estimator  mean     n std_err .config             
  <chr>   <chr>      <dbl> <int>   <dbl> <chr>               
1 rmse    standard   4.88      5  0.385  Preprocessor1_Model1
2 rsq     standard   0.616     5  0.0220 Preprocessor1_Model1

Application Exercise

05:00

1. Edit the code below to get the 5-fold cross validation error rate for the following model:

\(mpg = \beta_0 + \beta_1 horsepower + \beta_2 horsepower^2+ \epsilon\)

Auto_cv <- vfold_cv(Auto, v = 5)

results <- fit_resamples(lm_spec,
                         ----,
                         resamples = ---)

results |>
  collect_metrics()

• What do you think rsq is?

Answer

Auto_cv <- vfold_cv(Auto, v = 5)

results <- fit_resamples(lm_spec,
                         mpg ~ horsepower + I(horsepower^2),
                         resamples = Auto_cv)

results |>
  collect_metrics()

# A tibble: 2 × 6
  .metric .estimator  mean     n std_err .config             
  <chr>   <chr>      <dbl> <int>   <dbl> <chr>               
1 rmse    standard   4.38      5  0.110  Preprocessor1_Model1
2 rsq     standard   0.688     5  0.0177 Preprocessor1_Model1

Application Exercise

1. Fit 3 models on the data using 5 fold cross validation:

   \(mpg = \beta_0 + \beta_1 horsepower + \epsilon\)

   \(mpg = \beta_0 + \beta_1 horsepower + \beta_2 horsepower^2+ \epsilon\)

   \(mpg = \beta_0 + \beta_1 horsepower + \beta_2 horsepower^2+ \beta_3 horsepower^3 +\epsilon\)

2. Collect the metrics from each model, saving the results as results_1, results_2, results_3

3. Which model is “best”?

08:00